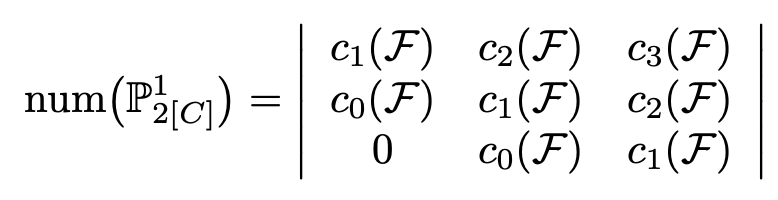|
Fermions and Supersymmetry in Neural Network Field Theories
|
|
There is an intricate connection between infinitely wide neural networks and bosonic field theories. In that limit, the random-parameter neural network corresponds to a Gaussian (free) field theory. We generalize and extend the correspondance by introducing fermionic field theories in the neural-network setting by introducing Grassmann-valued (so anti-commuting) weights. We show that such Grassmann neural networks obey an analogue of the Central Limit Theorem, where their statistics become Gaussian (in the sense of field theory), giving rise to a free fermionic field, i.e., the free Dirac spinor. |
|
more...
|
Improving Generative Inverse Design of Rectangular Patch Antennas With Test Time Optimization
|
|
Designing antennas for a target frequency response is often tedious: small changes in geometry (e.g. the width or thickness of a patch) can change many aspects of the radio-frequency response at once, so engineers typically need to rely on manual tuning or coarse heuristics. |
|
more...
|
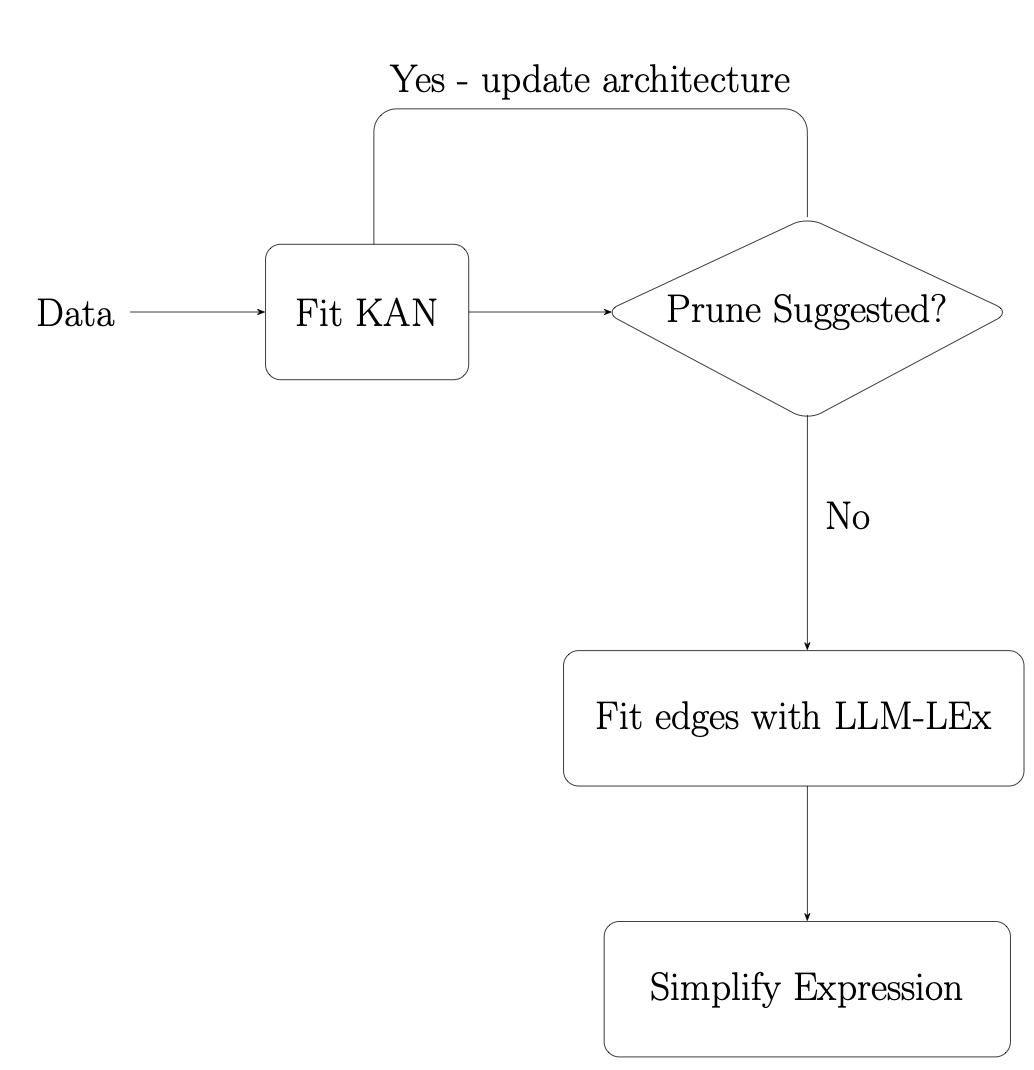
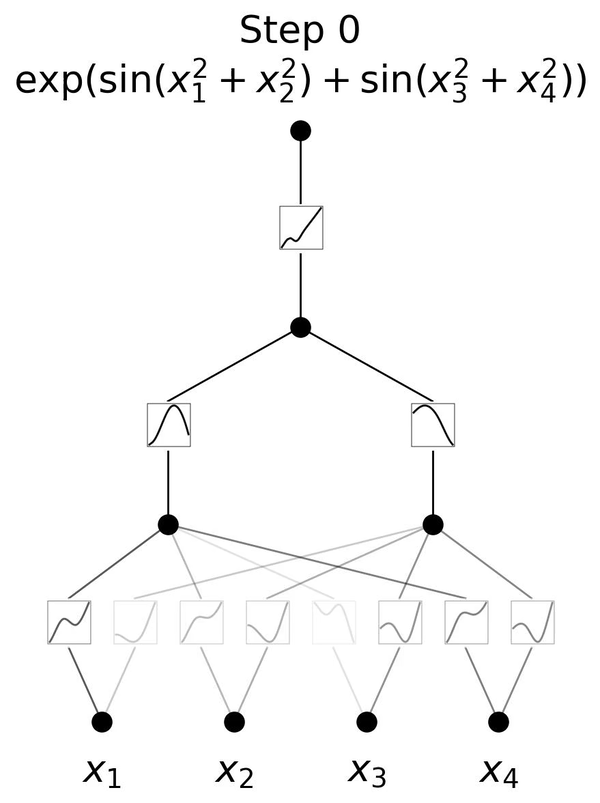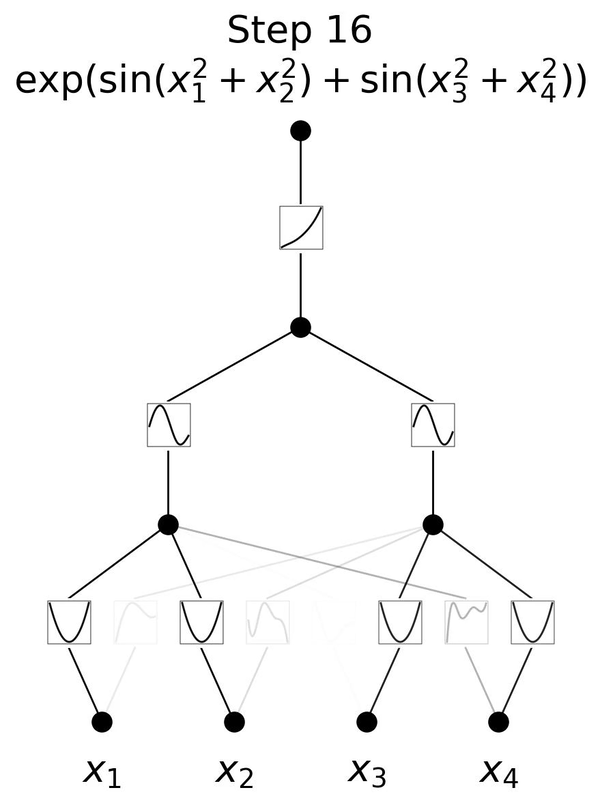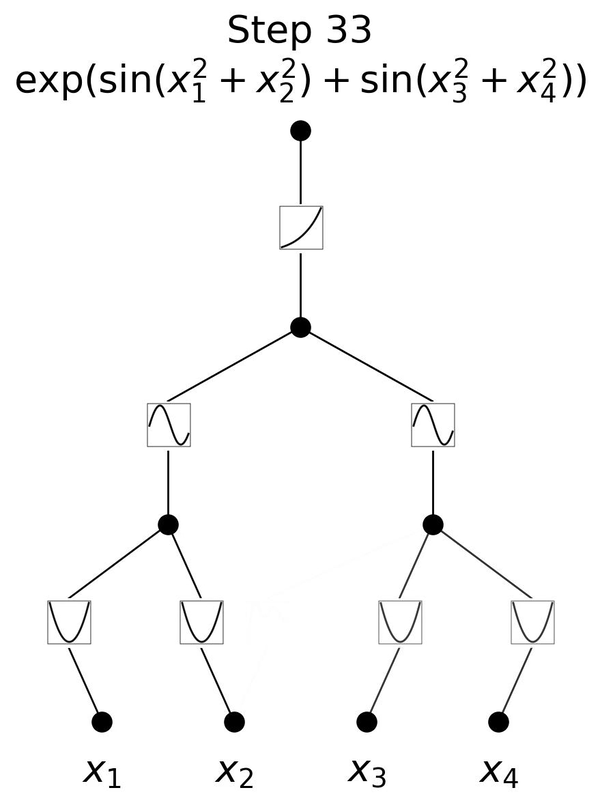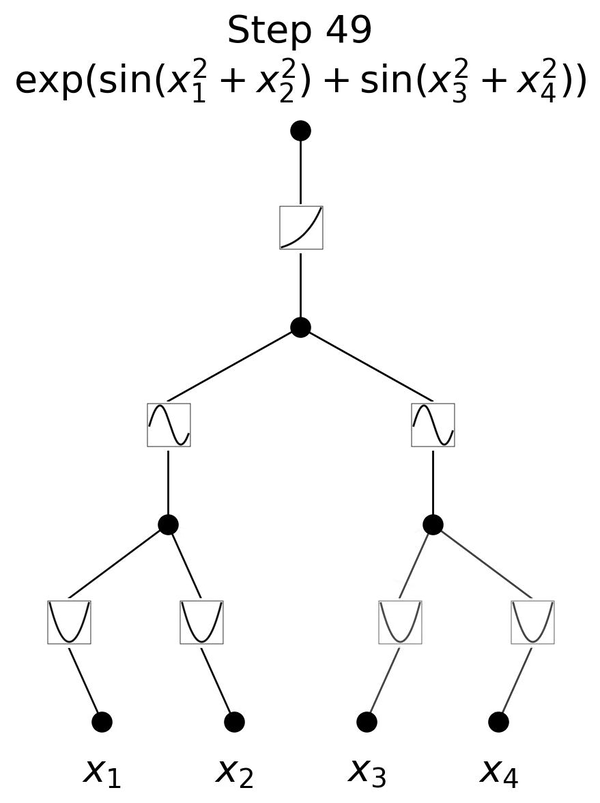
Symbolic Regression with Multimodal Large Language Models and Kolmogorov Arnold Networks
|
|
Symbolic regression is a process where, given some input and output data, one tries to infer an analytic function that can be used to obtain the output from the given input. This is crucial for interpreting black box functions such as neural networks. The challenge is that there is an endless possibility of combining or concatenating functions, and existing methods usually try to fit a pre-defined function basis. |
|
more...
|
Recent developments at the intersection of AI and Theoretical Physics
|
|
We discuss recent developments in artificial intelligence that are specifically geared towards application and scientific discovery in theoretical and mathematical physics. Along the way, we point out other phenomena at the intersection of Physics and AI, including chaos theory, phase transitions, spin glasses, symmetries, classical and statistical mechanics (see figure), and quantum theory. |
|
more...
|
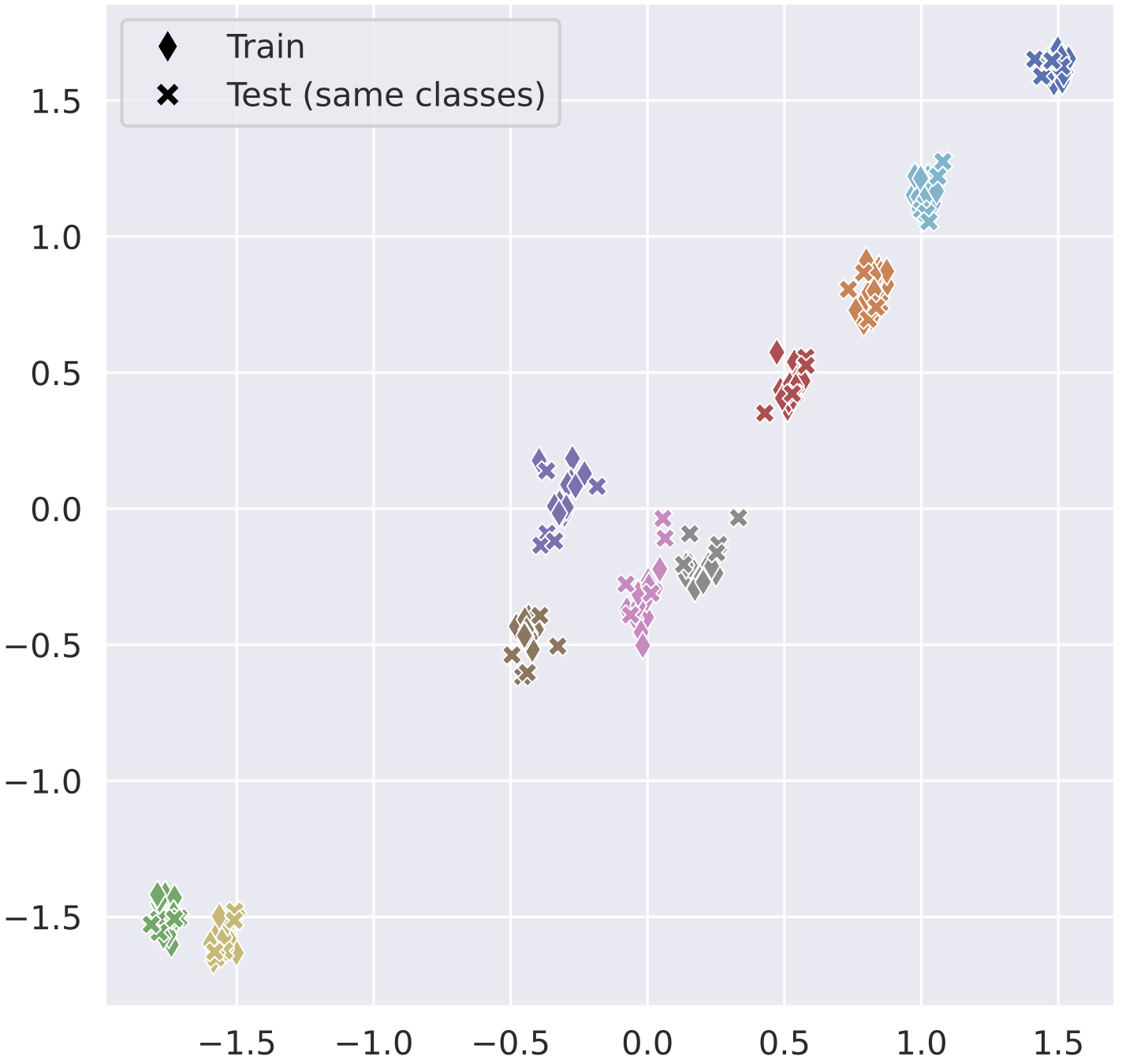
Learning Topological Invariance
|
|
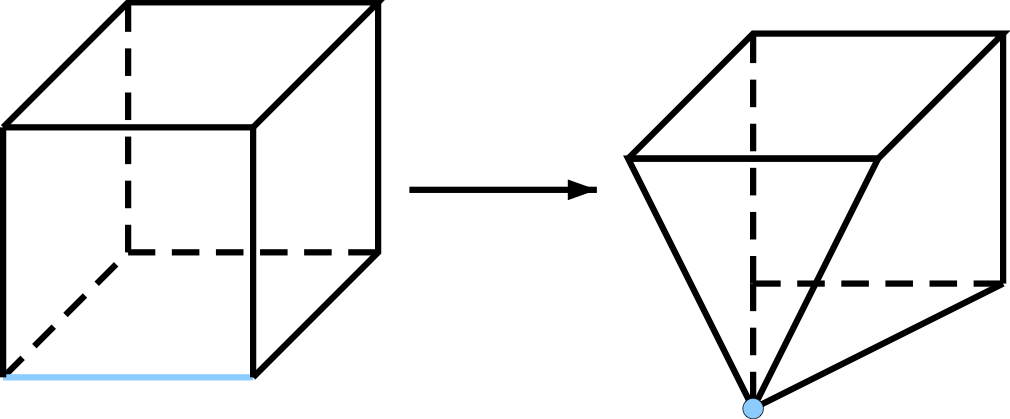
Topology is an equivalence relation where two spaces are equivalent if they differ by certain geometric deformations. We explore techniques to train a Neural Network to learn topological invariance, i.e., maps where an entire equivalence class is mapped to the same object, which we choose to be a vector in \(\mathbb{R}^N\), see first figure. By definition, this vector then corresponds to a topological invariant. We use contrastive learning as well as generative techniques with a transformer to achieve this. |
|
more...
|
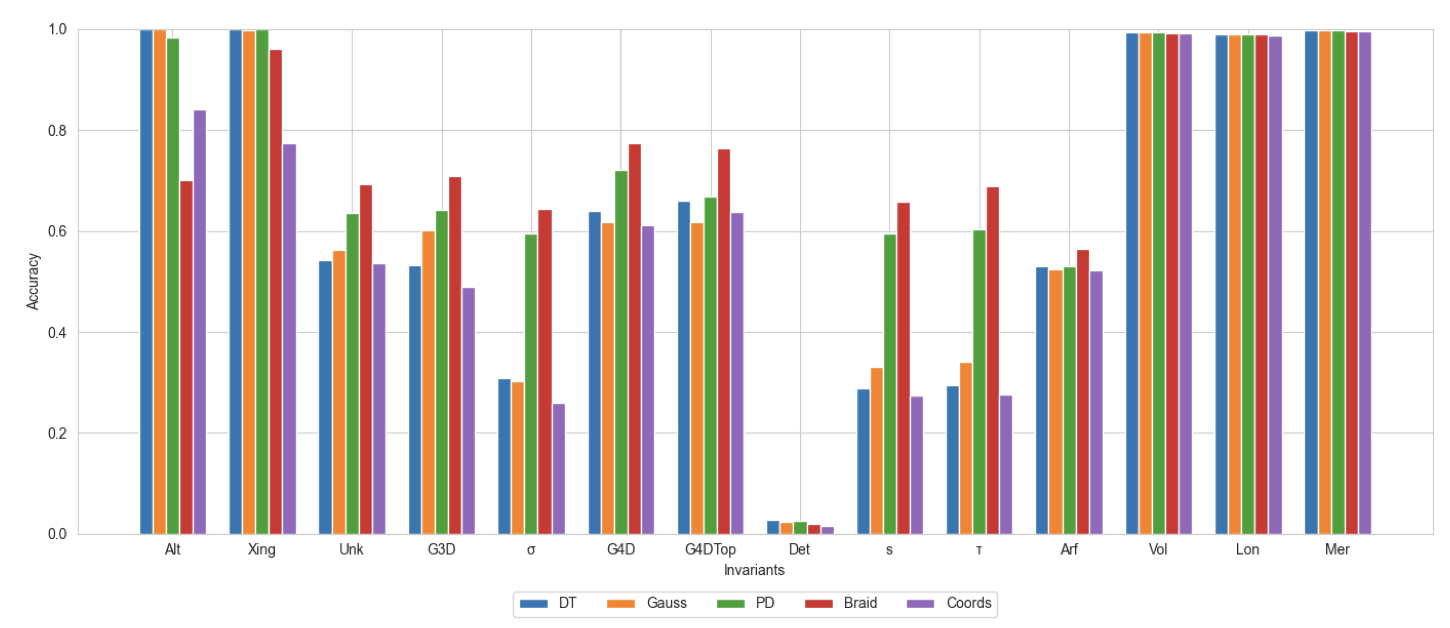
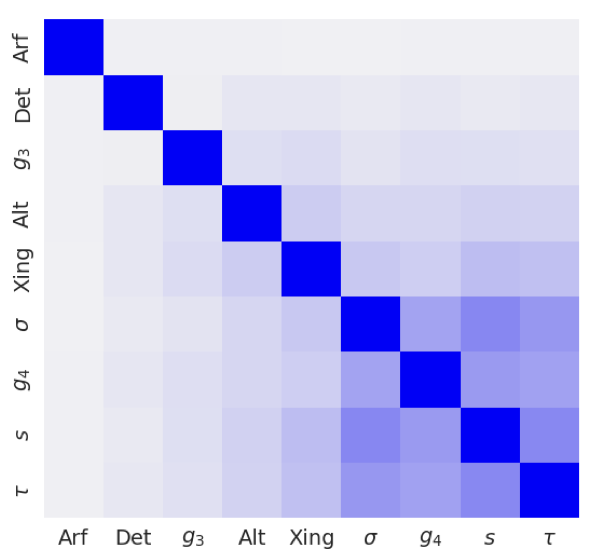
On the Learnability of Knot Invariants: Representation, Predictability, and Neural Similarity
|
|
Deciding whether two knots are can be smoothly deformed into one another is a central topic of low-dimensional topology. To this end many knot invariants have been proposed based on knot diagrams, geometric, and homological data. Moreover, many different encodings of knots have been used in the literature. In this paper, we ask which knot representations are most beneficial for a neural network to learn which invariants. Conversely, we also study which knot invariants can be learned to which degree. |
|
more...
|
Interpretable Machine Learning for Kronecker Coefficients
|
|
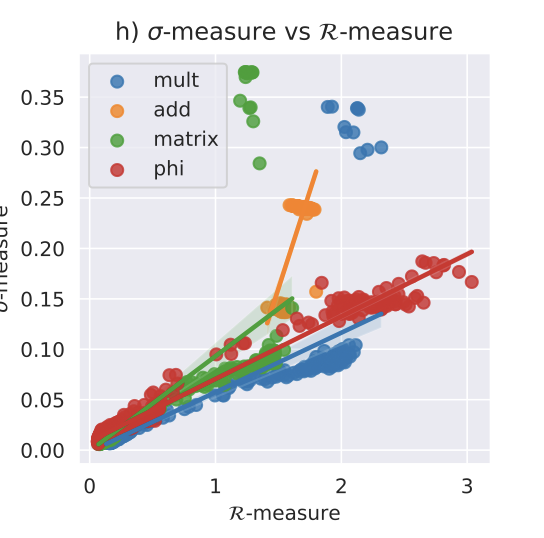
We study Kronecker coefficients which appear in the decomposition of representations of the symmetric group \(S_N\). These combinatorial objects are interesting from a computational complexity perspective: While determining whether the Littlewood–Richardson coefficients for \(GL_N(\mathbb{C})\) are vanishing is in P, the problem is NP hard for Kronecker coefficients. |
|
more...
|
Data for Mathematical Copilots: Better Ways of Presenting Proofs for Machine Learning
|
|
|
The datasets commonly used to train and test AI-based mathematical assistants—such as large language models—have significant limitations. Most notably, they tend to focus on relatively simple mathematics, rarely going beyond lower undergraduate-level content. They also rely on rigid evaluation methods, like binary correctness checks, which are insufficient for assessing AI capabilities in proof-based reasoning. |
|
more...
|
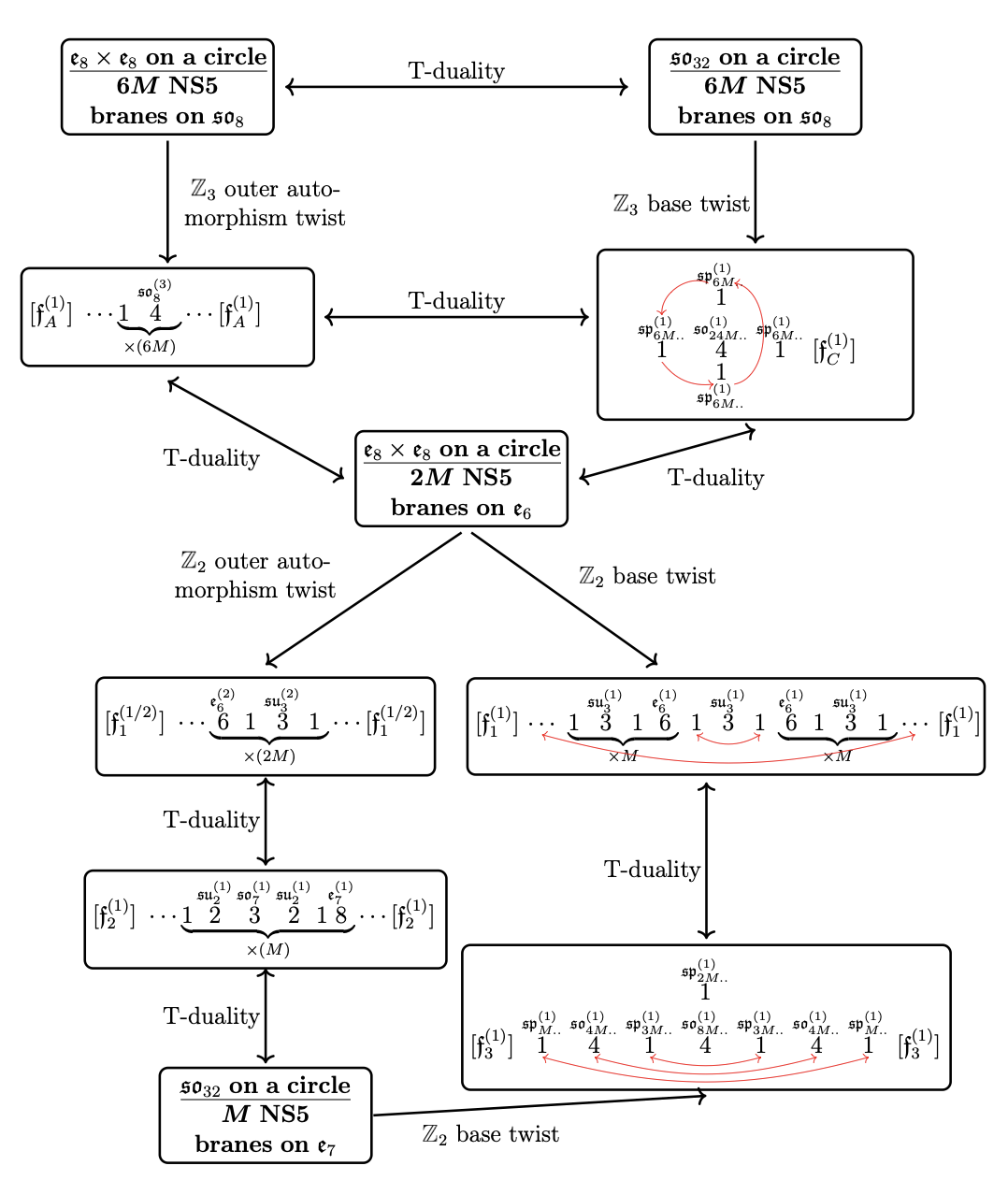
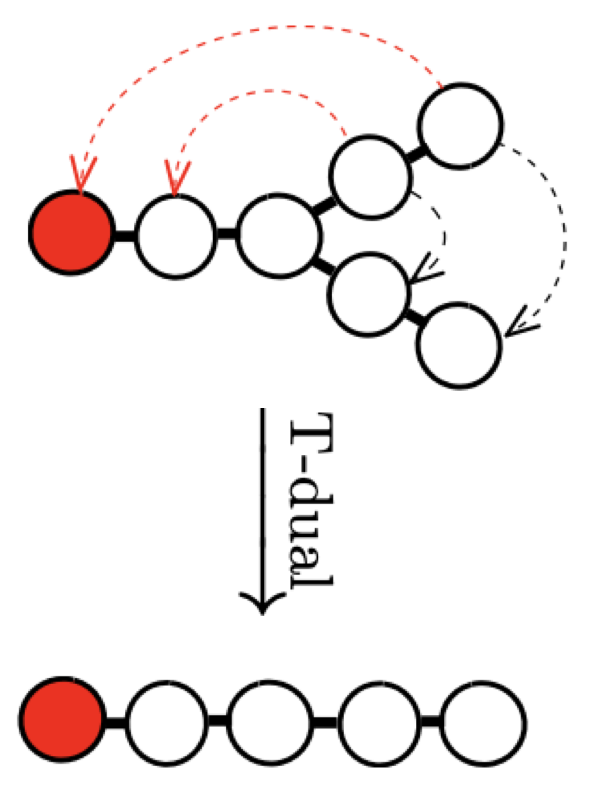
A Twist on Heterotic Little String Duality
|
|
In this work, we extend the known web of T-dualities among heterotic NS5-brane theories with eight supercharges by introducing new types of twists. These twists involve reordering certain gauge and flavor symmetries, as well as permuting tensor multiplets when compactifying on a circle. To systematically compare different T-dual theories, we identify key properties that remain unchanged under duality—such as the structure of the Coulomb branch, higher-group symmetries, and the ranks of flavor symmetry groups. |
|
more...
|
Attractors, Geodesics, and the Geometry of Moduli Spaces
|
|
We study a series of recent conjectures using the attractor mechanism. First, we observed in [2304.00027] a relation between attractor points and degeneracies in the spectrum of the scalar Laplacian. A recent conjecture by Etheridge [2311.18693] states that the eigenvalues of the scalar Laplacian with respect to the Calabi-Yau metric are eigenfunctions of the Laplacian on the moduli space with respect to the Weil-Petersson metric. We show that this is true for \(T^2\), but fails for some BPS states in \(T^4\). |
|
more...
|
A Heterotic Kähler Gravity and the Distance Conjecture
|
|
We study deformations of the cubic superpotential in heterotic string theory. Since the theory is at most quadratic in the moduli fields, we can integrate them out and obtain a new holomorphic theory, which shares similarities with Kodaira-Spencer gravity and holomorphic Chern-Simons theory. In the topological theory, a certain combination of H-flux and the holomorphic top form take on the role of the metric, and we define quantities such as the Hodge star \(\star_H\) with respect to this object. We also introduce a new symplectic cohomology theory where the complex structure deformation plays the role of the symplectic form (see image). |
|
more...
|
Bounds and Dualities of Type II Little String Theories
|
|
In this paper, we continue our study of 6D LSTs, but this time we look at Type II LSTs. In contrast to the Heterotic LSTs of [2311.02168], Type II LSTs have a much more constrained flavor sector. In fact, we use a mix of anomaly inflow arguments and unitarity constraints from the worldsheet theory of the little string, as well as some group theory, to argue that the rank of the flavor symmetry can be at most 2. |
|
more...
|
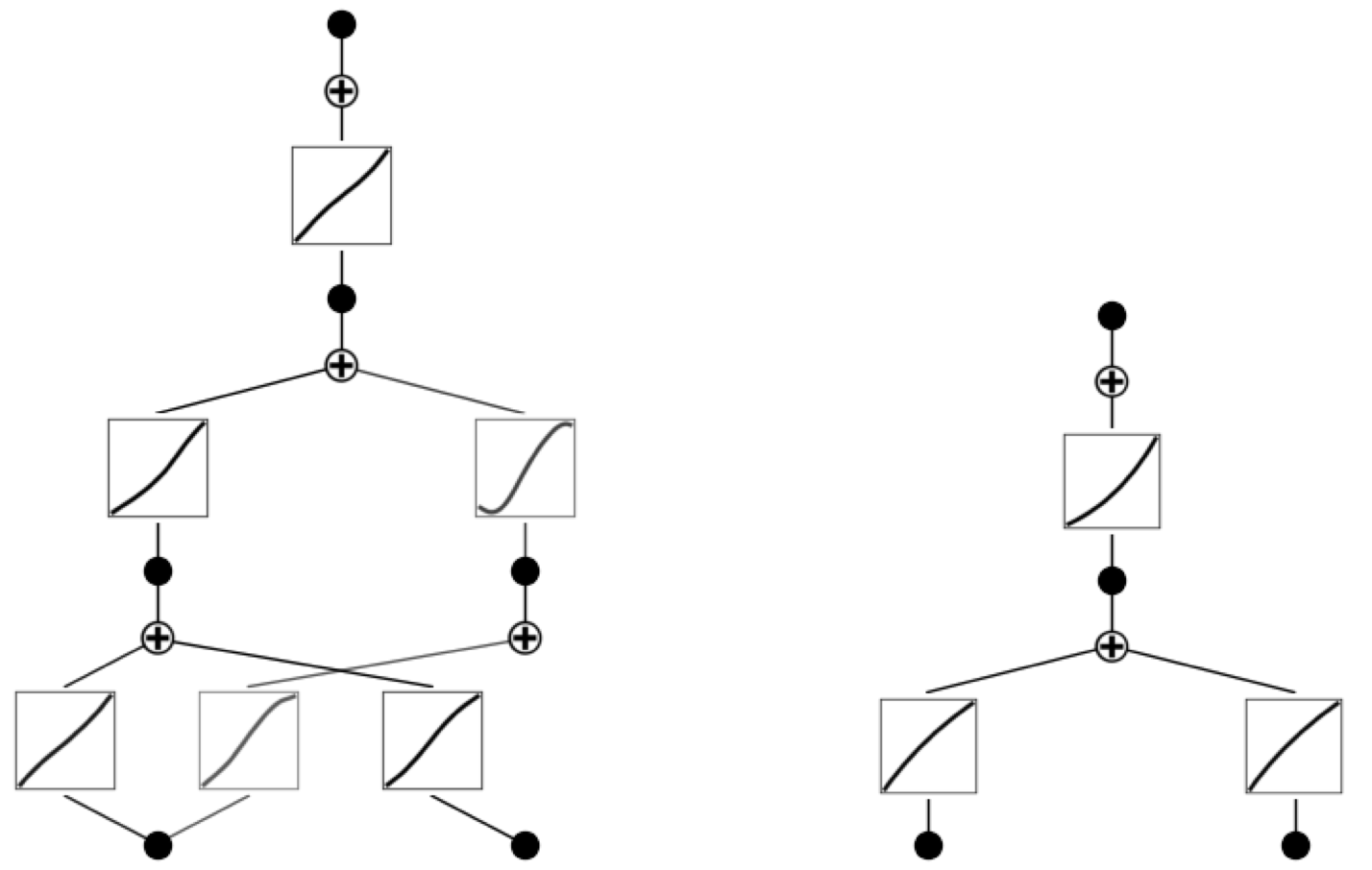
KAN: Kolmogorov-Arnold Networks
|
|
We introduce a new type of neural network, called KAN, as an alternative to standard feed-forward neural networks. They are based on Kolmogorov-Arnold representation theory, which means for our purposes that we can represent any function by a collection of piece-wise cubic polynomials (so-called cubic splines). In contrast to standard NNs, this means that the function basis is fixed (to be piece-wise cubic) rather than learned from weights plus activation functions, so we only have to tune the parameters that control the individual cubic splines. While this is more expensive than a standard NN, KANs typically can get away with much fewer parameters, thus offsetting the cost. Moreover, their piecewise nature prevents catastrophic forgetting which plagues NNs. Fewer parameters also mean that KANs are much more interpretable, see the animation for an example. |
|
more...
|
The Frozen Phase of Heterotic F-theory Duality
|
|
String Theory (more precisely F-Theory) has been used to construct consistent supergravity theories in six dimensions. In addition to the classical theories with ADE gauge groups, the landscape contains more exotic theories as well. One set of such theories is known as theories with frozen singularities. Essentially, there is a discrete flux which prevents the singularities from becoming smooth. This phenomenon is related to so-called O7+ branes in Type IIB string theories, models without vector structure in Heterotic SO(32) string theory, and the CHL string in Heterotic E8 theory. While F-theory allows to study all of them via duality, the construction remains complicated. For example, for F-theory, a model with an O7- brane and 4 D7 branes on top (which is a standard SO(8) gauge theory) looks equivalent to (meaning this has the same monodromy as) a model with a single O7+ brane. |
|
more...
|
On classical de Sitter solutions and parametric control
|
|
The question of whether well-controlled de Sitter solutions exist, and if so whether they can be obtained from string theory, remains an open and much-discussed topic. In this paper, we study string theory compactifications on a specific class of 6D manifolds called solv-manifolds. Loosely speaking, these are Lie groups (and hence, they are also manifolds) with an underlying lattice that makes the manifold compact. Topologically, they are torus fibrations, and mathematicians have classified all possibilities. The advantage of using these constructions over other Calabi-Yau constructions is that the geometry can be described very explicitly in terms of the Lie algebra structure constants. |
|
more...
|
Rigor with Machine Learning - from Field Theory to the Poincare Conjecture
|
|
|
Machine learning techniques are notoriously difficult to interpret and often produce stochastic results. For these reasons, fields like pure mathematics and formal theoretical physics are "late adopters" of these techniques. In this invited contribution to Nature Reviews, we describe how we can harness the power of ML despite these challenges. |
|
more...
|
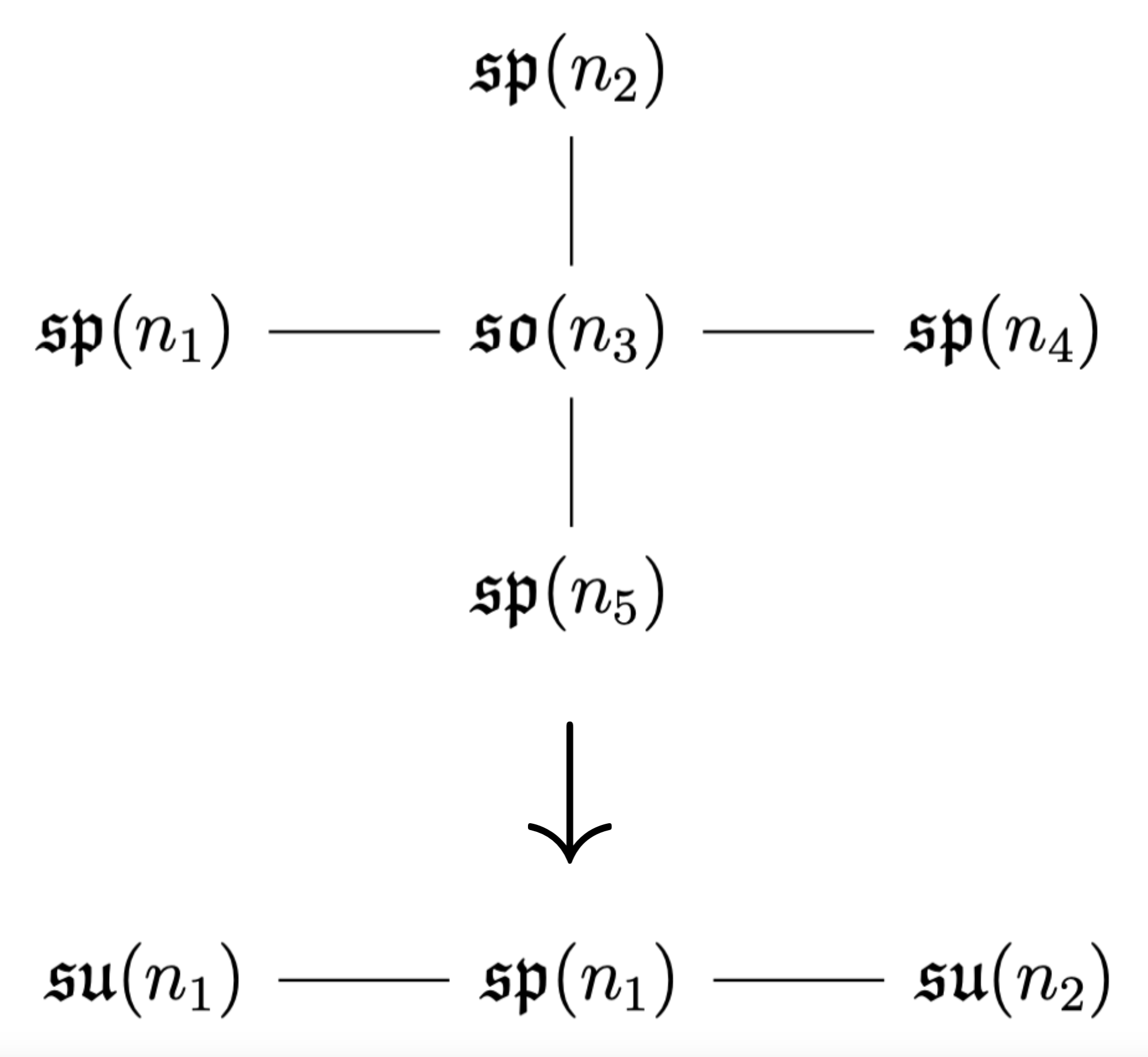
T-Duality and Flavor Symmetries in Little String Theories
|
|
We study six-dimensional little string theories (LSTs) as well as their circle compactifications to 5D. It is known that different 6D theories can become the same theory in 5D under T-duality, and it is interesting to ask which 6D quantities are preserved under this duality. Some quantities like the Coulomb branch dimension and the two-group structure constants have been argued to be invariants under the duality, and we argue that the rank of the flavor group of the 6D theories is preserved as well. |
|
more...
|
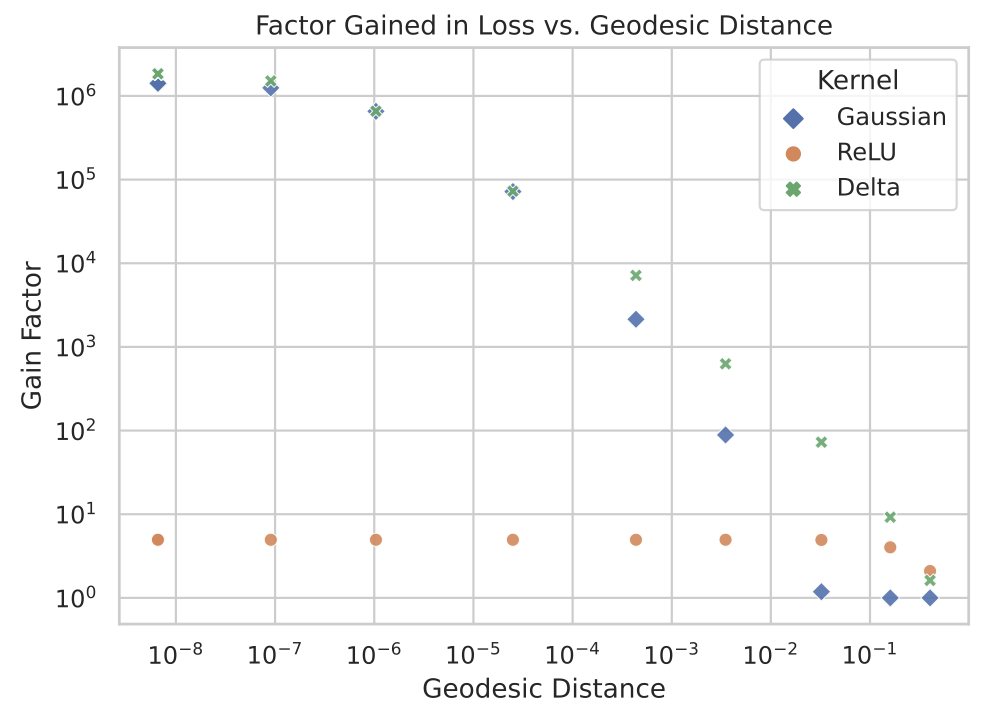
Metric Flows with Neural Networks
|
|
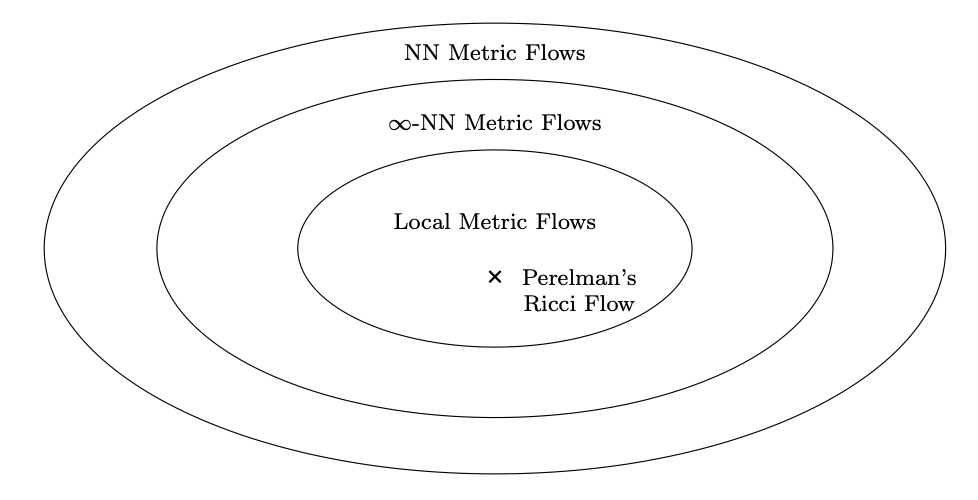
We consider metric flows, which means that the metric on some space changes dynamically following its equations of motion. Mathematicians have studied such flows extensively, i.e., the metric changes proportional to the gradient of some action or energy functional. The perhaps best-known flow is Perelman's Ricci flow, which he used to prove the 3D Poincare conjecture, but other flows exist such as the Mabuchi flow or the Calabi-flow for Kähler metrics. |
|
more...
|
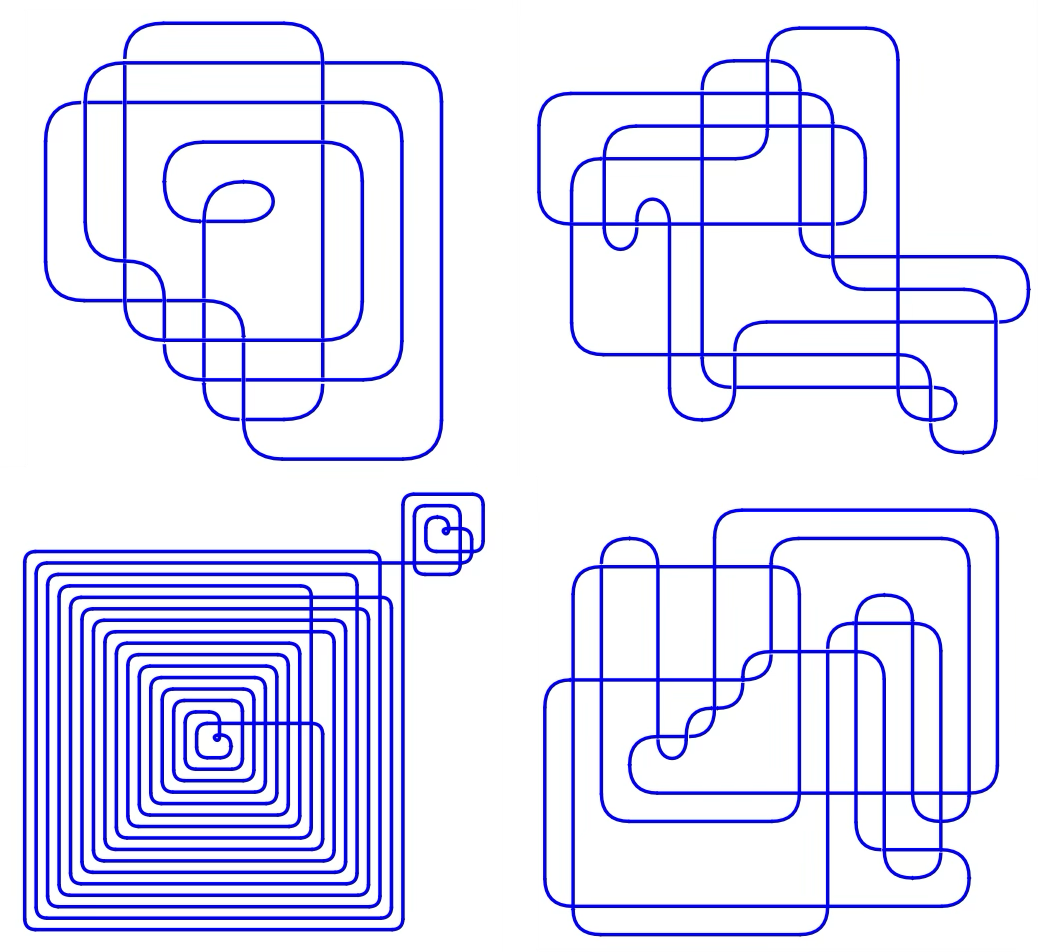
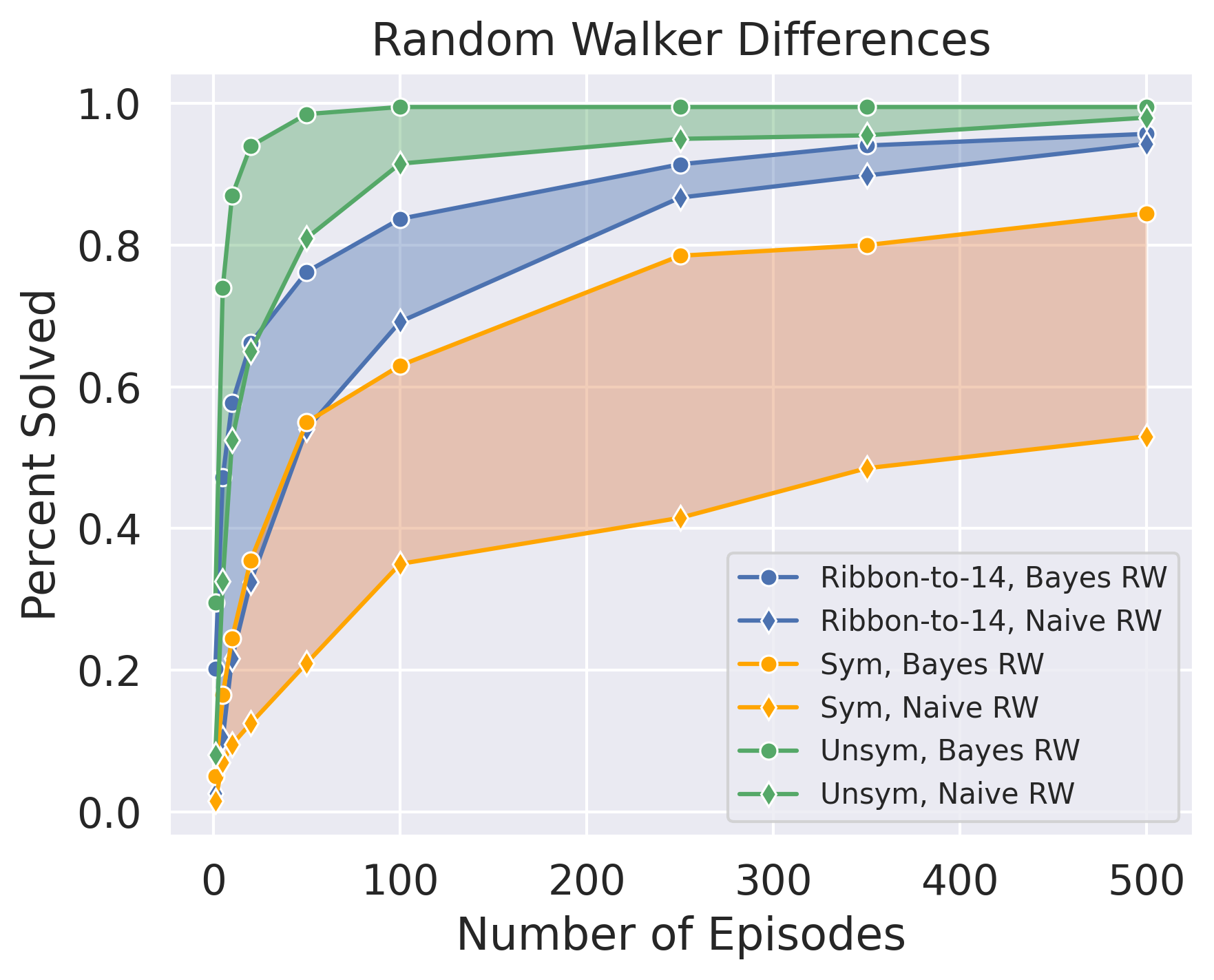
Searching for ribbons with machine learning
|
|
A knot is a closed (knotted) string embedded in a three-dimensional space (a three-sphere, say). As such, it is the boundary of some surface in the three-sphere, see the first figure. If this surface is a disk, the knot is called slice. A closely related object is a ribbon knot: roughly, a knot is ribbon if you can cut it open at two positions and put a band in between the cuts such that you obtain a collection of circles. Every ribbon knot is slice, but it is an open conjecture whether every slice knot is ribbon. |
|
more...
|
Level Crossings, Attractor Points and Complex Multiplication
|
|
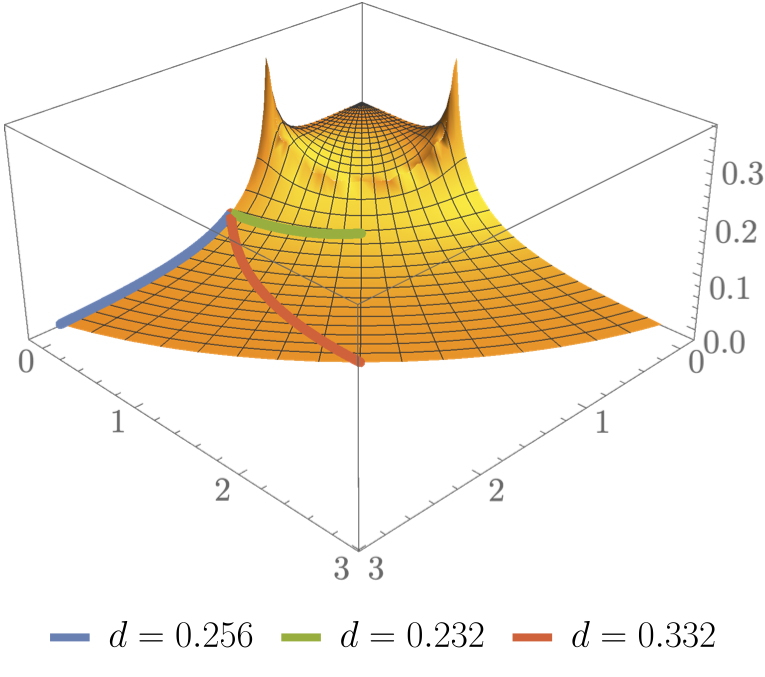
In a previous paper, Anthony and I observed that the eigenmodes of the scalar Laplacian run up and down as a function of the shape (complex structure) of the compact extra dimensions of string theory (Calabi-Yau (CY) manifolds). In particular, this means that the eigenvalues cross at some points. This begs the question: What is special about these crossing points? |
|
more...
|
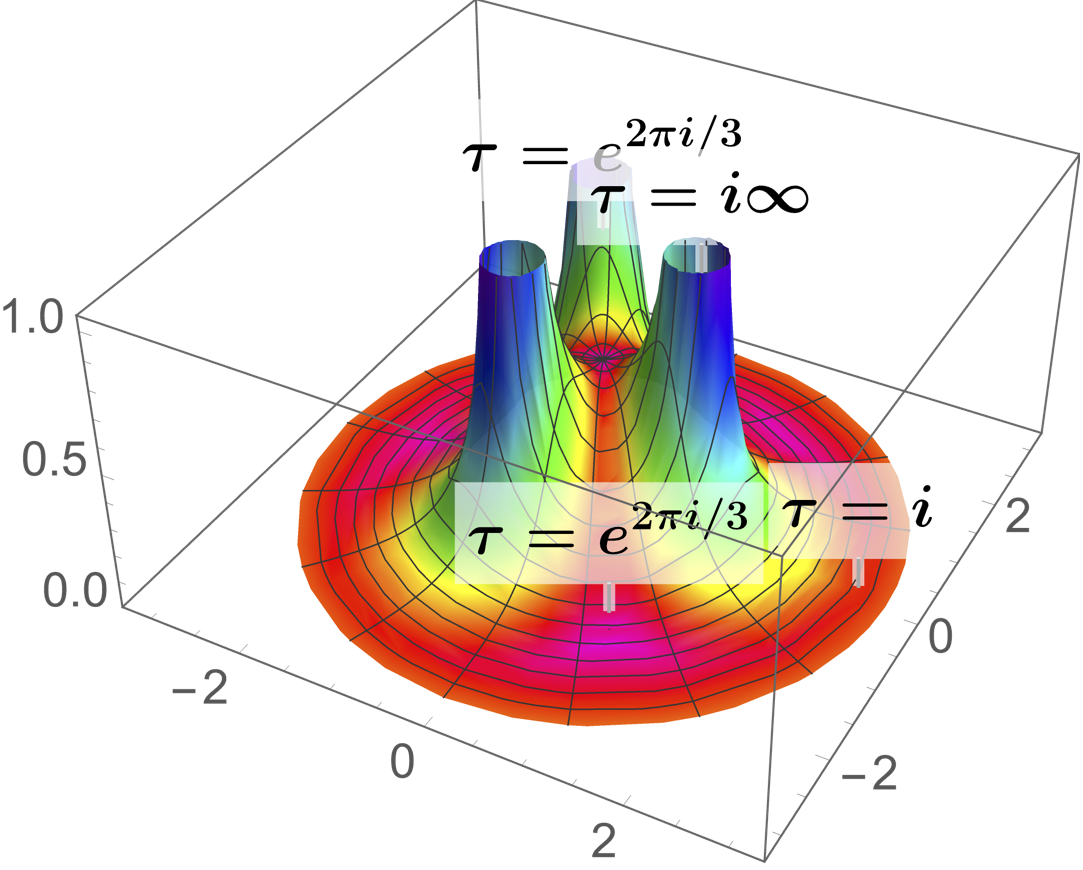
Symmetries of Calabi-Yau Prepotentials with Isomorphic Flops
|
|
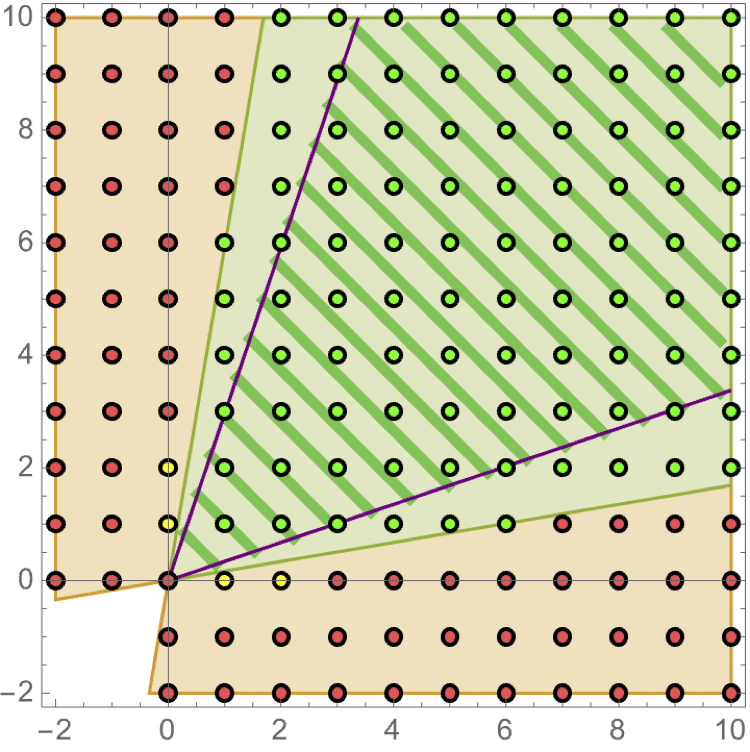
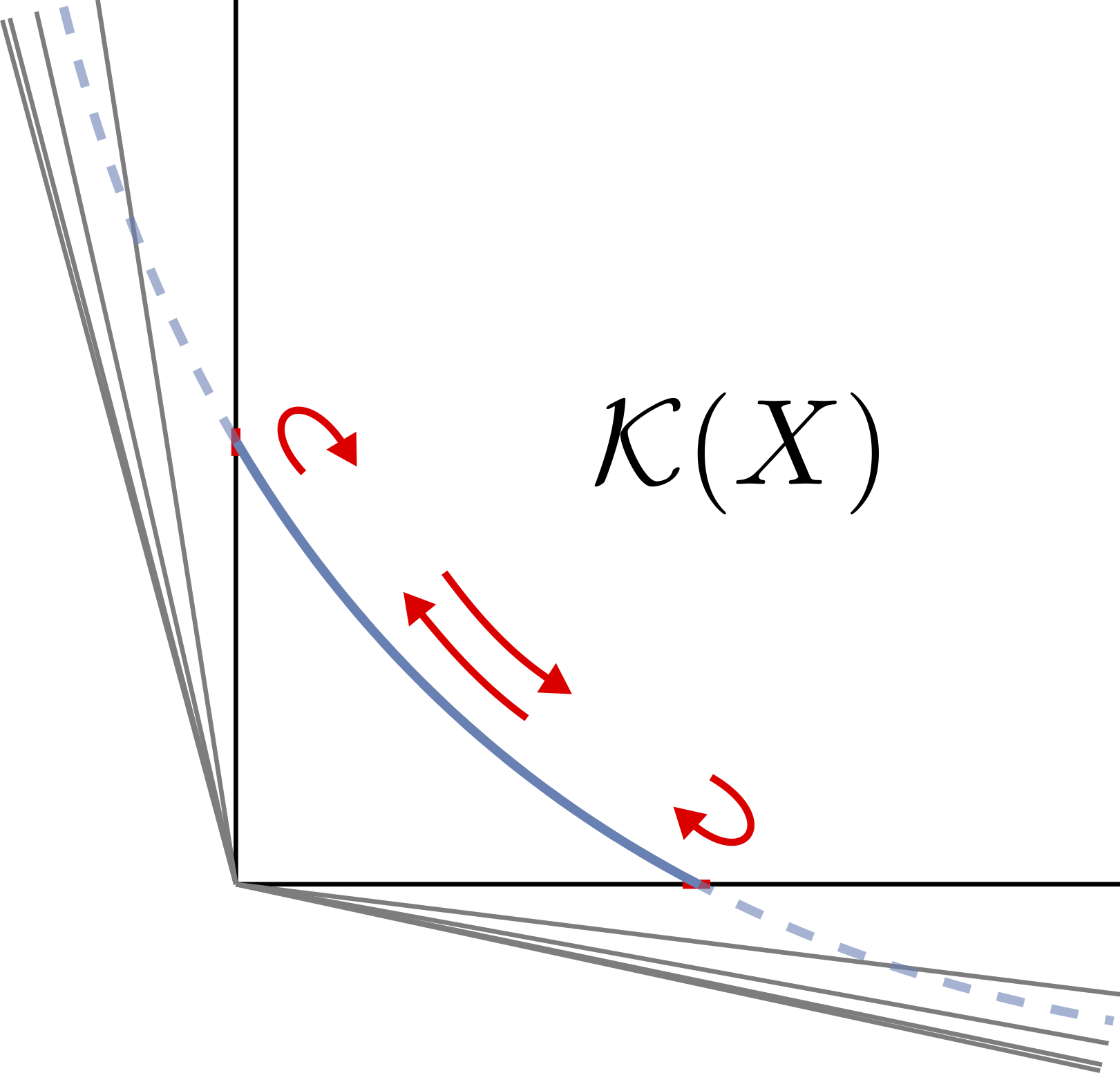
In his seminal paper, Coxeter wrote in 1934: "[Take] three vertical mirrors, erected on the sides of an equilateral triangle so as to form a prism, open at the top. A candle placed within this prism gives rise to an unlimited number of images." This was generalized shortly thereafter by Vinberg to the case where the mirrors do not necessarily form a prism, but more generally a polyhedron or cone. Among cones string theorists deeply care about are Kahler cones and their duals, called Mori cones. We noticed recently that topological transitions across Kahler cone walls of Calabi-Yau (CY) manifolds exist which lead to new CYs that are isomorphic to the old one. The Kahler cone of such a space after the transition is obtained by reflection along the corresponding Kahler cone wall. It is easy to construct spaces with multiple such "reflecting Kahler cone walls", giving rise to infinitely many equivalent (isomorphic) CYs, whose (infinitely many) individual Kahler cone glues to one big Kahler cone, and we explain how to describe them in terms of Coxeter groups. For 3 Kahler cone walls, this is illustrated (on the hyperbolic Poincare Disk) in the figure on the left. |
|
more...
|
Flops for Complete Intersection Calabi-Yau Threefolds
|
|
We discuss flops in projective Complete Intersection Calabi-Yau manifolds. We explain that there are two different types of flops, whose presence and type can be read off from the GLSM charges. Of course, this can also be used to engineer manifolds that exhibit a certain flop type.
|
|
more...
|
Recent Developments in Line Bundle Cohomology and Applications to String Phenomenology
|
|
This is a conference proceeding to the Nankai Symposium on Mathematical Dialogues: In celebration of S.S.Chern's 110th anniversary.
We review progress in deriving closed-form expressions for line bundle cohomologies and discuss applications to string phenomenology. We also review results from the papers [2104.03325], [2108.10323], and [2112.12106] on the structure and properties of the extended Kahler cone of CICY manifolds.
|
|
more...
|
Learning Size and Shape of Calabi-Yau Spaces
|
|
For the NeurIPS ML and the Physical Sciences workshop, we presented our library cymetric to compute Calabi-Yau metrics for any projective complete intersection Calabi-Yau or toric Kreuzer-Skarke Calabi-Yau.
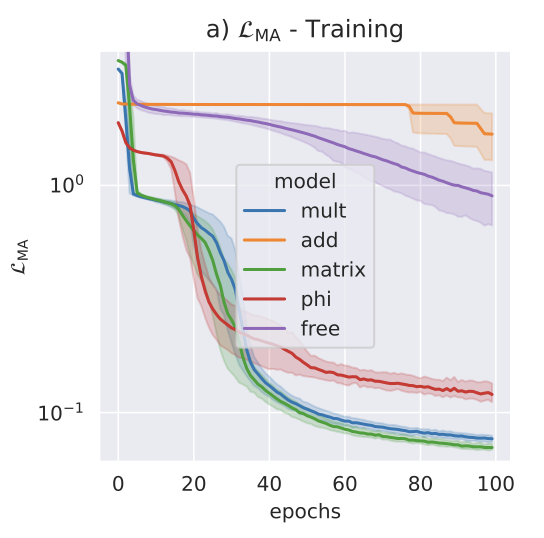
We vastly extend to scope by implementing general point sampling methods on the CY with known distributions for any toric or projective ambient space (i.e. for any \(h^{1,1}\)). We also introduce a new architecture, the "Phi Model", which allows to find the Ricci flat metric in a fixed Kahler class.
|
|
more...
|
Geodesics in the extended Kähler cone of Calabi-Yau threefolds
|
|
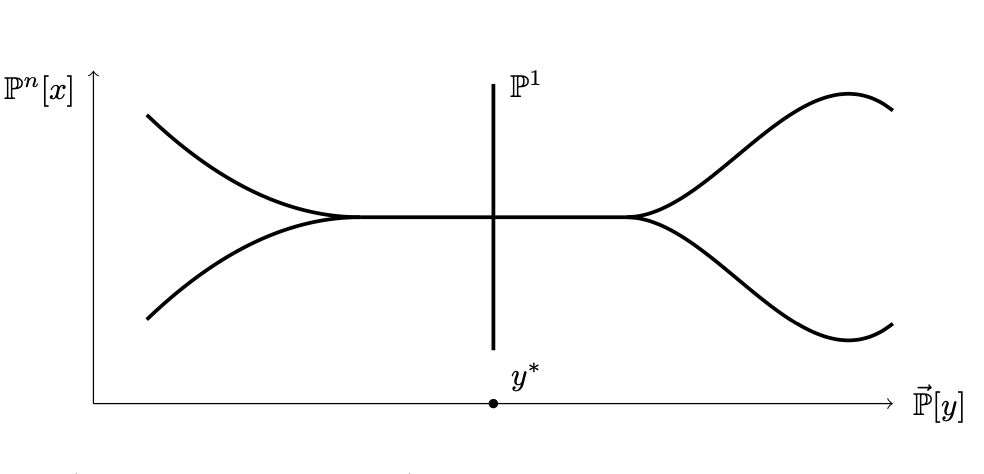
We continue our study of the moduli space of a Calabi-Yau (CY) and the topology changes that can occur. We find that as one traverses the moduli space, three things can happen:
|
|
more...
|
String Pheno 2021
|
|
In the week of July 12th to July 16th 2021, Northeastern is hosting the 20th installment of the anual String Phenomenology conference, the largest conference in this field. Due to the pandemic, the conference takes place virtually.
It covers a range of topics, including
|
|
more...
|
A blood atlas of COVID-19 defines hallmarks of disease severity and specificity
|
|
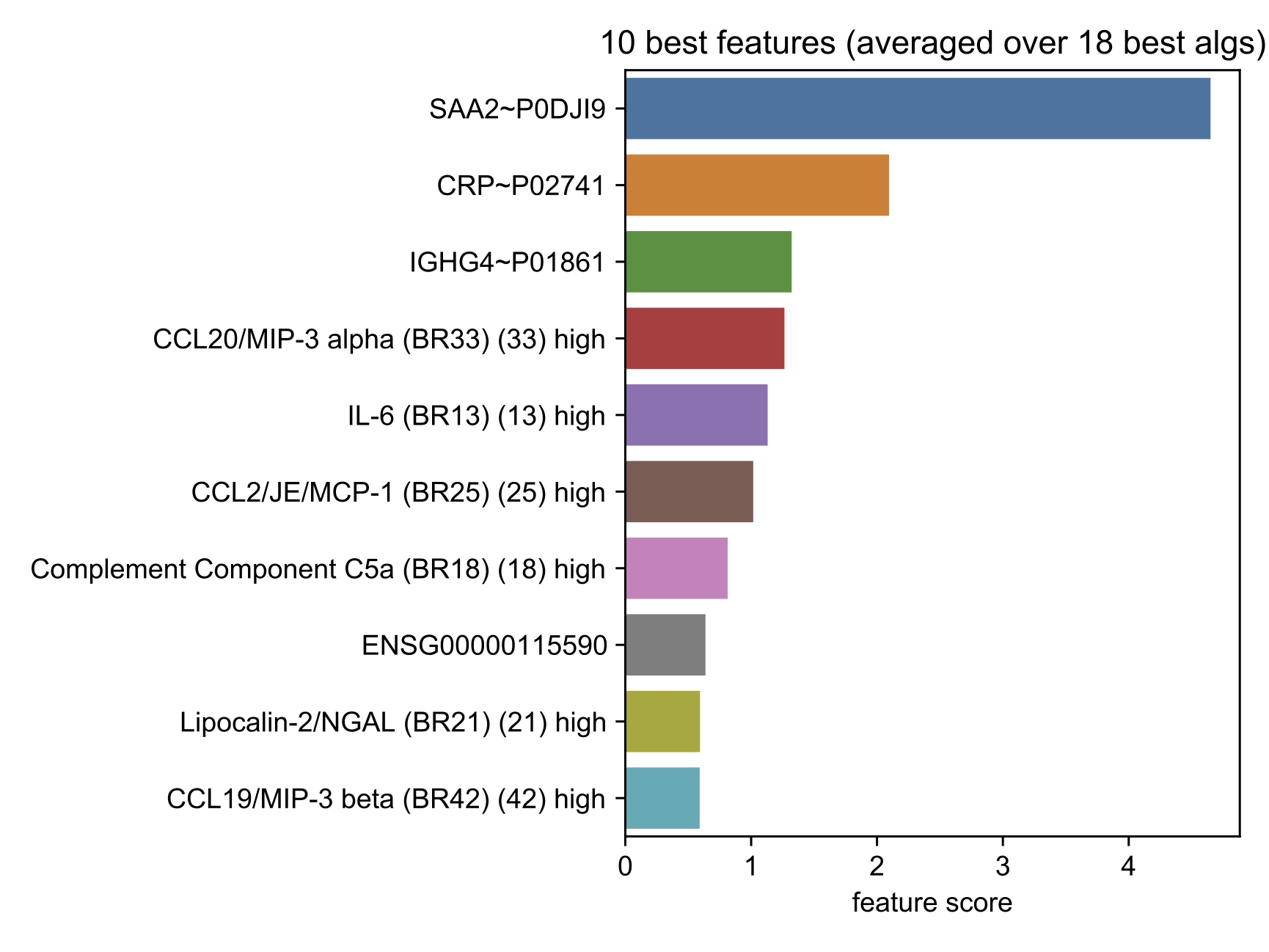
In a collaboration with biologists, clinicians, and mathematicians, we studied various aspects of COVID19. I used ML to answer two questions: |
|
more...
|
Swampland Conjectures and Infinite Flop Chains
|
|
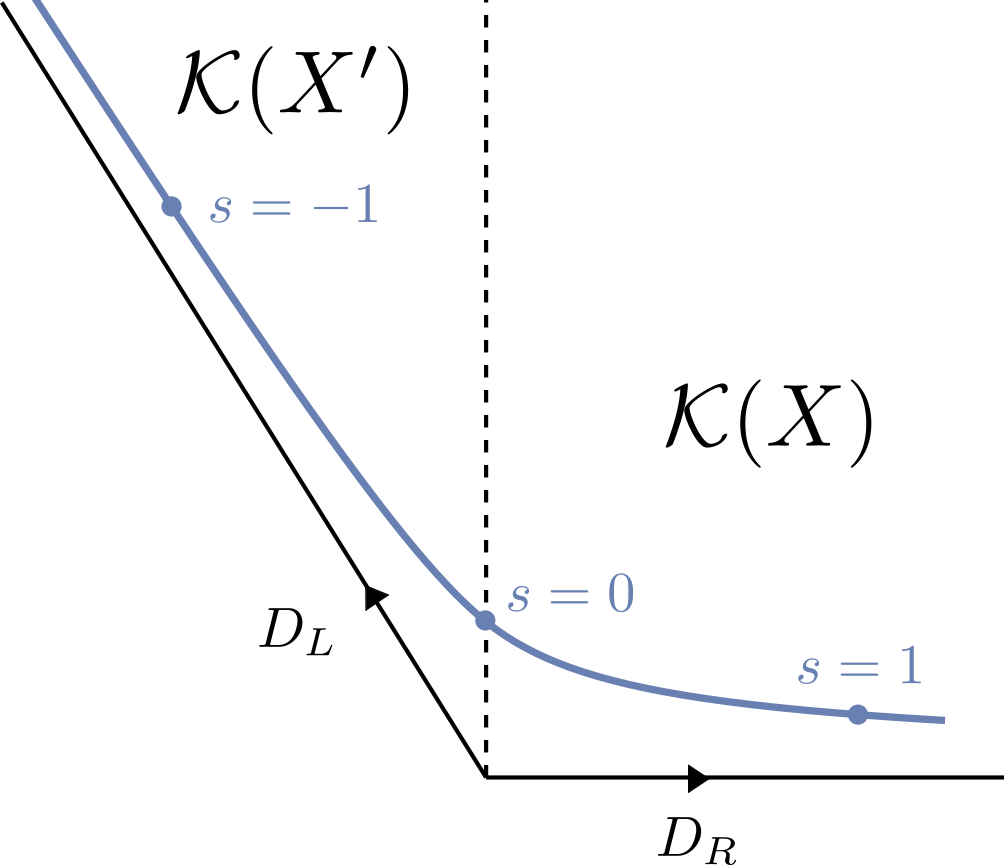
As you walk through the moduli space of a Calabi-Yau (CY), the CY can change its topology. Very common topological transitions are flops. Flops can lead to new or to equivalent CYs, and there are even cases where infinitely many flops occur. This begs the question:
|
|
more...
|
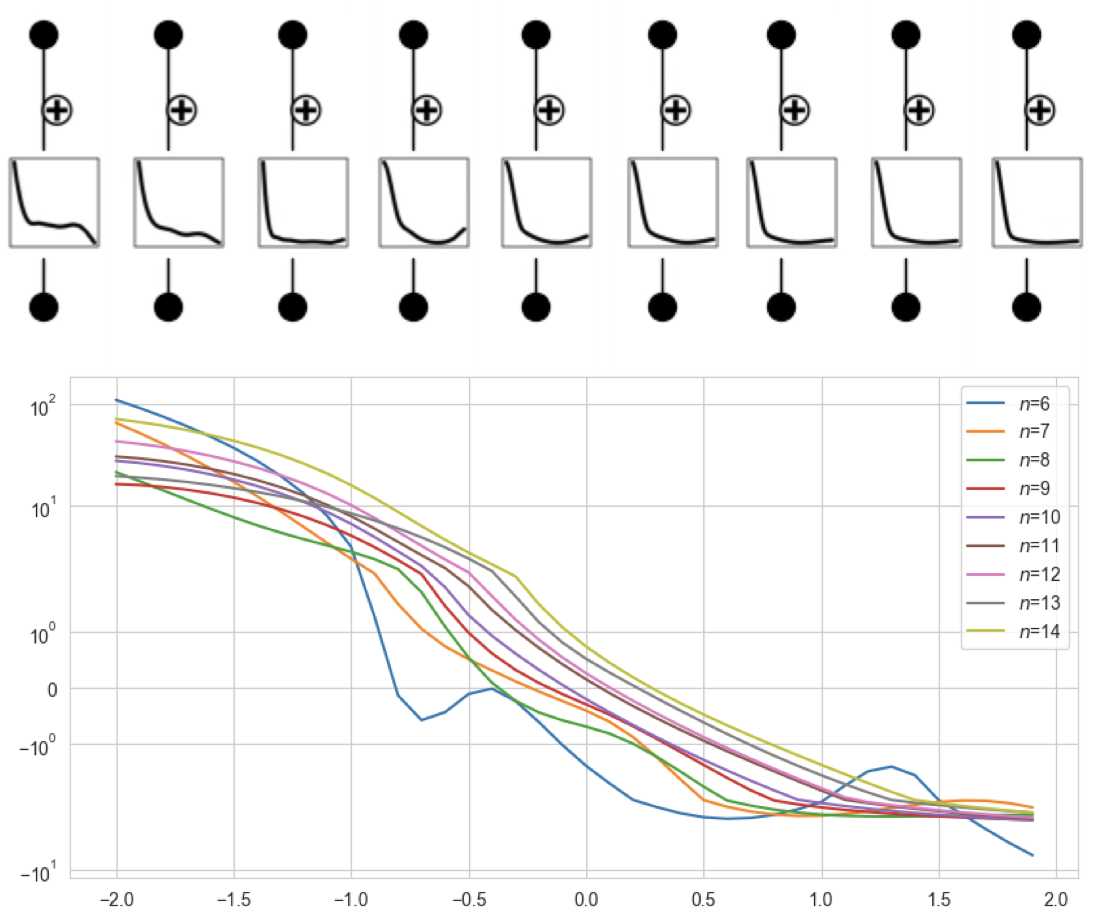
Moduli-dependent KK towers and the Swampland Distance Conjecture on the Quintic
|
|
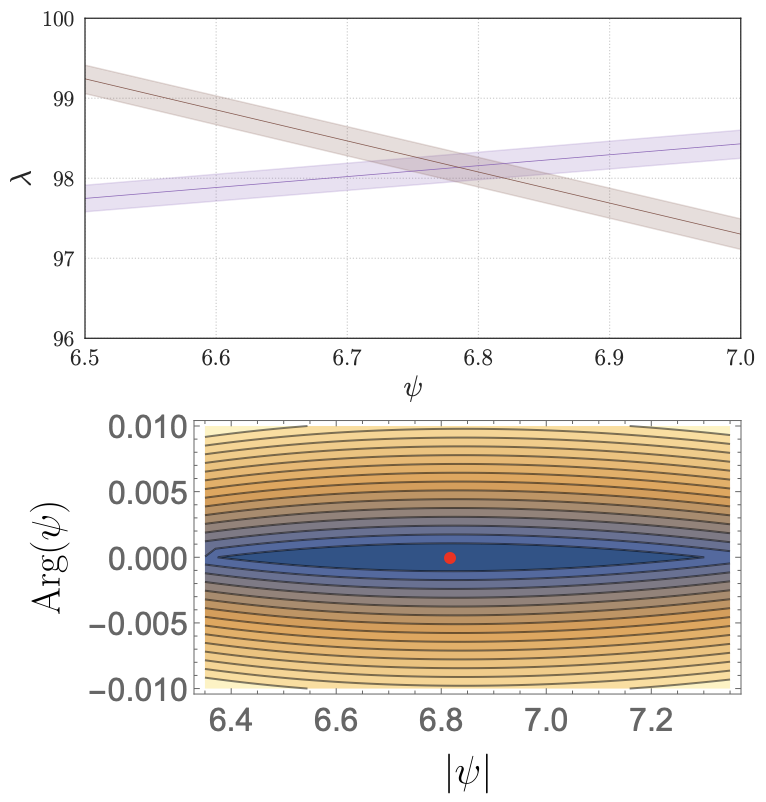
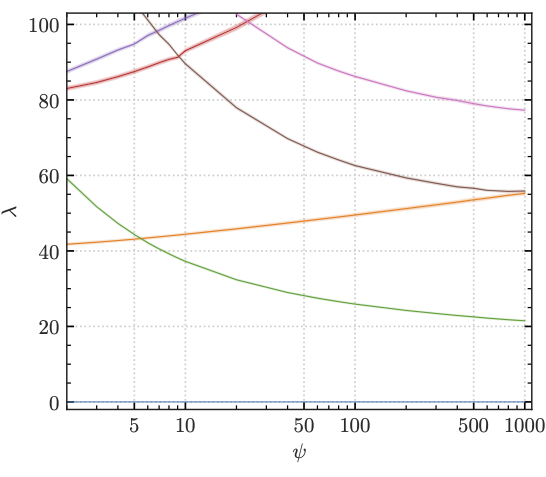
Take for example the Klein-Gordon equation \(g^{ab}\partial_a\partial_b \varphi = m^2\varphi\). We see that the massive spectrum depends on the metric. We can compute moduli-dependent Calabi-Yau metrics, and hence we can compute (moduli-dependent) massive KK states on Calabi-Yau manifolds. The swampland distance conjecture tells us that this KK tower should become exponentially light when moving \(O(1)\) distance (in Planck units) in moduli space (see top image). In this paper, we compute geodesics in moduli space to see what it means to move \(O(1)\) in terms of the parameters that describe the CY. |
|
more...